[TOC]
动态规划-数字三角形模型
不同题目的逻辑关系:
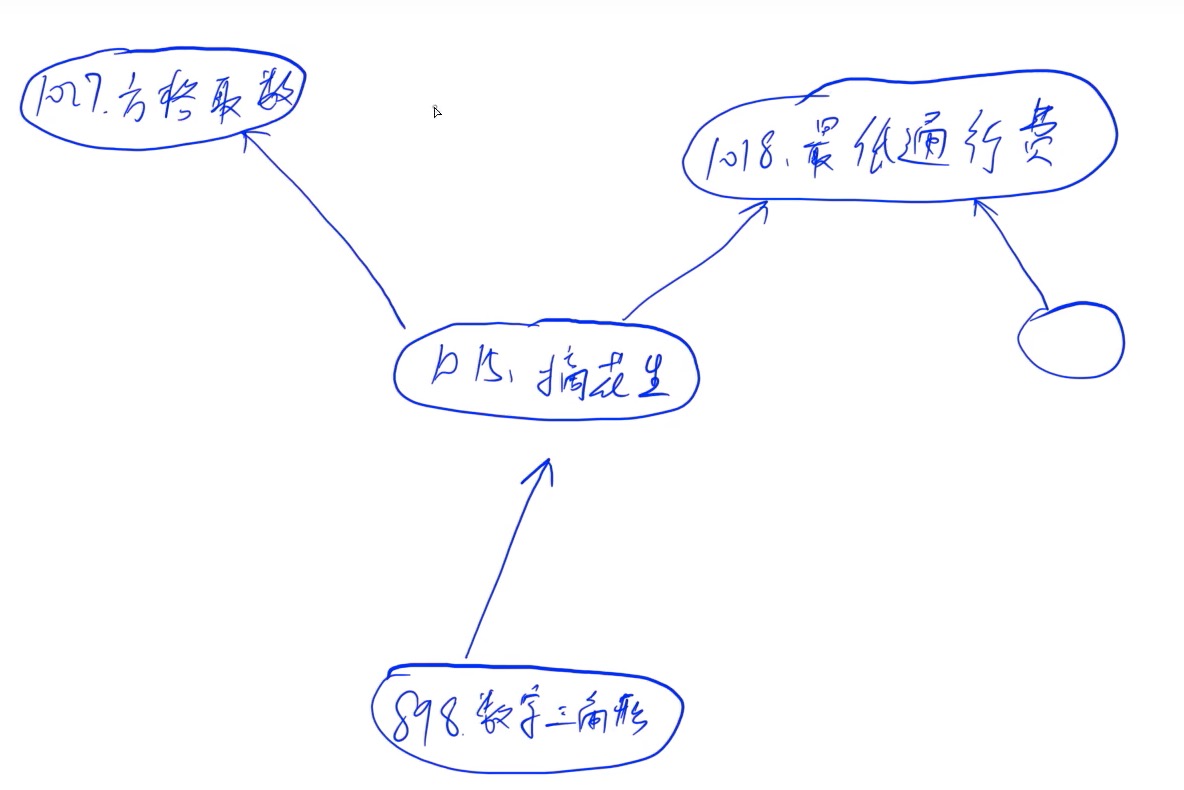
摘花生
从集合角度来考虑DP问题–闫氏思考法
算法里的坐标画法:
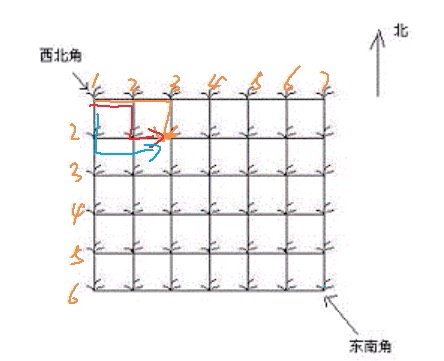
f(2, 3)表示的是所有从(1, 1)走到(2, 3)的路线,存在属性是max。
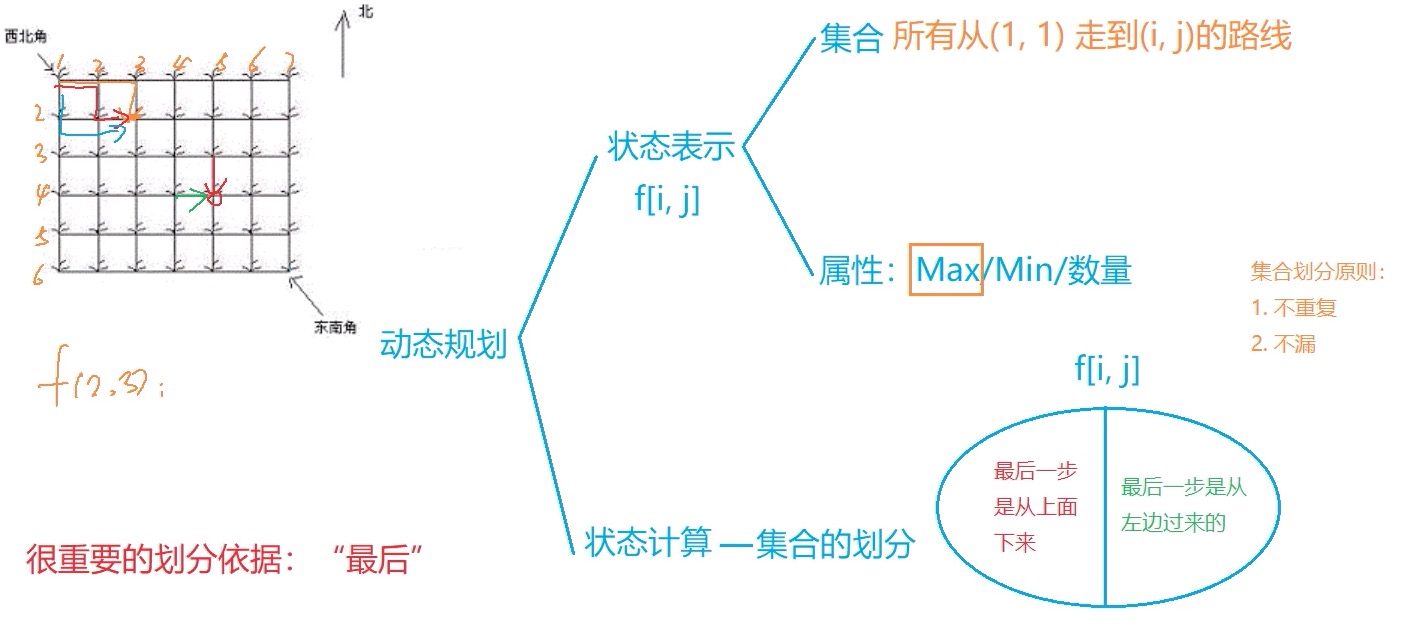
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int m;
int w[N][N], f[N][N];
int main()
{
cin >> m;
while (m --)
{
int x, y;
cin >> x >> y;
for (int i = 1; i <= x; i ++)
for (int j = 1; j <= y; j ++)
scanf("%d", &w[i][j]);
for (int i = 1; i <= x; i ++)
for (int j = 1; j <= y; j ++)
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
cout << f[x][y] << endl;
}
}
最低通行费
N * N 的网格, 限制在 2N - 1的时间,在规定时间内,至少需要的费用。(从左上角走到右下角)
从左上角走到右上角,时间不超过2N - 1意味着什么?
不走回头路的情况下就需要2N - 1的时间,所以意味着不能走回头路
// 因为是求min,要考虑一些边界问题和f[i][j]的状态转换问题。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, INF = 1e9;
int m;
int w[N][N], f[N][N];
int main()
{
int x;
cin >> x;
// 一个是从上面走下来,一个是从左边走过来。不能从外部走进来。因为外部走进来是0肯定是更小的。
for (int i = 1; i <= x; i ++)
for (int j = 1; j <= x; j ++)
{
// 如果是第一行第一列,那就是本身 特判左上角
scanf("%d", &w[i][j]);
if (i == 1 && j == 1) f[i][j] = w[i][j];
else
{
// 因为求min还是要把f[i][j]置成极大值才能置换
f[i][j] = INF;
// 只有不在第一行的时候,才能从上面过来
if (i > 1) f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
// 只有不在第一列的时候,才能从左边过来
if (j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
}
}
cout << f[x][x] << endl;
}
方格取数
从左上角走到右下角,走过的数字置零,并且把数字收集。一共走两次。找出两条这样的路径,让和最大。

走两次:
f[i1, j1, i2, j2] 表示从所有(1, 1),(1, 1)分别走到(i1, j1),(i2, j2)的路径的最大值。
如何处理“同一个格子不能被重复选择”?(同时走的思路)

只有在i1 + j1 == i2 + j2 时, 两条路径的格子才可能重合。
f[k, i1, i2] 表示从所有(1, 1),(1, 1)分别走到(i1, k - i1),(i2, k - i2)的路径的最大值。
注:k == i1 + j1 == i2 + j2; k 表示的是两条路线走到格子的横纵坐标之和。
集合的状态:
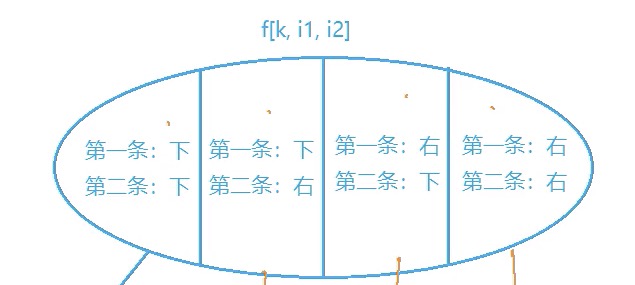
两条路线从上往下走的最大值:

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int n;
int w[N][N], f[N * 2][N][N];
int main()
{
cin >> n;
int a, b, c;
while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
for (int k = 2; k <= 2 * n; k ++)
for (int i1 = 1; i1 <= n; i1 ++)
for (int i2 = 1; i2 <= n; i2 ++)
{
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
int t = w[i1][j1];
if (i1 != i2) t += w[i2][j2];
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
cout << f[n + n][n][n] << endl;
}
附录:
屈婉玲 离散数学 三部曲

摘花生问题的终极版,K取方格数。走k次,如果用方格取数来做,每多一次就多一维。10条路线,就要考虑1000种情况,所以用最小费用流来做。
本质来说,动态规划问题是图论里的一部分。