[TOC]

DeepLearning.ai-0201-正交化-正则化-Dropout-初始化等

Train/Dev/Test sets

数据分成三个部分：Train/Dev/Test sets。有时候可以只有Train/Dev。
训练样本和测试样本尽量来自同一分布。
通常设置Train sets和Test sets的数量比例为70%和30%。
对于大数据样本，Train/Dev/Test sets的比例通常可以设置为98%/1%/1%，或者99%/0.5%/0.5%。样本数据量越大，相应的Dev/Test sets的比例可以设置的越低一些。

Bias/Variance

偏差/方差代表欠拟合/过拟合
一般来说，Train set error体现了是否出现bias，Dev set error体现了是否出现variance（正确地说，应该是Dev set error与Train set error的相对差值）

这一块可以再次理解下怎么通过这两个error来计算偏差和方差的思想，train error高的话，说明模型没学习到位，肯定出现了高偏差，出现了欠拟合。

如果train error 和 dev error相对差值高的话，说明高方差，模型在训练集上表现更好，在测试集表现更差，出现了过拟合。

假设Train set error为1%，而Dev set error为11%，即该算法模型对训练样本的识别很好，但是对验证集的识别却不太好。这说明了该模型对训练样本可能存在过拟合，模型泛化能力不强，导致验证集识别率低。
假设Train set error为15%，而Dev set error为16%，虽然二者error接近，即该算法模型对训练样本和验证集的识别都不是太好。这说明了该模型对训练样本存在欠拟合，就是高偏差的表现。
假设Train set error为15%，而Dev set error为30%，说明了该模型既存在high bias也存在high variance（深度学习中最坏的情况）
假设Train set error为0.5%，而Dev set error为1%，即low bias和low variance，是最好的情况。

Basic Recipe for Machine Learning

防止欠拟合和过拟合的方法

降低high bias的方法（欠拟合）：
- 增加神经网络的隐藏层个数、神经元个数
- 训练时间延长
- 选择其它更合适的更合适的NN模型
降低high variance的方法（过拟合）：
- 增加训练样本数据（数据增强）
- 进行正则化Regularization（L1、L2正则化，Dropout)参数的选择比较复杂
- 选择其他更复杂的NN模型
- Early stoping（提早停止训练网络）通过减少训练次数来防止过拟合，这样J就不会足够小
- Dropout

正交化

机器学习训练模型有两个目标：一是优化cost function，尽量减小J；二是防止过拟合。这两个目标彼此对立的，即减小J的同时可能会造成过拟合，反之亦然。我们把这二者之间的关系称为正交化orthogonalization。

解决high bias和high variance的方法是不同的。实际应用中通过Train set error和Dev set error判断是否出现了high bias或者high variance，然后再选择针对性的方法解决问题。
Bias和Variance的权衡问题：
- 传统机器学习算法中，Bias和Variance通常是对立的，减小Bias会增加Variance，减小Variance会增加Bias。
- 深度学习中，通过使用更复杂的神经网络和海量的训练样本，一般能够同时有效减小Bias和Variance。这也是深度学习之所以如此强大的原因之一。

Regularization

L1、L2正则化的基础概念

Logistic regression的L2 regularization表达式：

\[\begin{array}{l}{J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{2}^{2}} \\ {\|w\|_{2}^{2}=\sum_{j=1}^{n_{x}} w_{j}^{2}=w^{T} w}\end{array}\]

为什么只对w进行正则化而不对b进行正则化呢？

其实也可以对b进行正则化。但是一般w的维度很大，而b只是一个常数。相比较来说，参数很大程度上由w决定，改变b值对整体模型影响较小。b只是众多参数的一个，所以，一般都忽略它。

Logistic regression的L1 regularization表达式，就是各个元素的绝对值之和。

\[\begin{array}{l}{J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{1}} \\ {\|w\|_{1}=\sum_{j=1}^{n_{x}}\left|w_{j}\right|}\end{array}\]

与L2 regularization相比，L1 regularization得到的w更加稀疏，即很多w为零值。其优点是节约存储空间，因为大部分w为0，但实际上也并没有节约太多空间。L1 regularization在解决high variance过拟合方面比L2 regularization并不更具优势，L1的在微分求导方面比较复杂。所以，一般L2 regularization更加常用。

L2正则化在深度学习中的具体应用

深度学习的L2 regularization表达式：

\[\begin{array}{l}{J\left(w^{[1]}, b^{[1]}, \cdots, w^{[L]}, b^{[L]}\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum_{l=1}^{L}\left\|w^{[l]}\right\|^{2}} \\ {\left\|w^{[l]}\right\|^{2}=\sum_{i=1}^{n^{[l]}} \sum_{j=1}^{n^{l-1}}\left(w_{i j}^{[l]}\right)^{2}}\end{array}\]

\(\lambda\)就是正则化参数，需要在数据集中验证选择最优的\(\lambda\)。
通常把\(\left\|\boldsymbol{w}^{[l]}\right\|^{2}\)称为Frobenius范数，记为\(\left\|\boldsymbol{w}^{[l]}\right\|_{F}^{2}\)。范数的计算方法，就是各个元素的平方和：

\[\|A\|_{F}=\sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n}\left|a_{i j}\right|^{2}}\]

L2 regularization也被称做权重衰减。因为它使得在参数更新的时候，\(\boldsymbol{w}^{[l]}\)的梯度有个增量，导致更新\(\boldsymbol{w}^{[l]}\)的时候减去那个增量，使\(\boldsymbol{w}^{[l]}\)比没有正则化的时候小。

\[\begin{aligned} w^{[l]} & :=w^{[l]}-\alpha \cdot d w^{l l} \\ &=w^{[l]}-\alpha \cdot\left(d w_{b e f o r e}^{[l]}+\frac{\lambda}{m} w^{[l]}\right) \\ &=\left(1-\alpha \frac{\lambda}{m}\right) w^{[l]}-\alpha \cdot d w_{b e f o r e}^{[l]} \end{aligned}\]

															Remind:$$1-\alpha \frac{\lambda}{m}<1$$

正则化如何避免过拟合的？

如果使用L2 regularization，当\(\lambda\)很大时，\(\boldsymbol{w}^{[l]} \approx 0\)。意味着该神经网络模型中的某些神经元实际的作用很小，可以忽略。从效果上来看，其实是将某些神经元给忽略掉了。这样原本过于复杂的神经网络模型就变得不那么复杂了，而变得非常简单化了。如下图所示，整个简化的神经网络模型变成了一个逻辑回归模型。问题就从high variance变成了high bias了。

因此，选择合适大小的\(\lambda\)值，就能够同时避免high bias和high variance，得到最佳模型。

Dropout

Dropout是指在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃。也就是说，每次训练时，每一层都有部分神经元不工作，起到简化复杂网络模型的效果，从而避免发生过拟合。

Inverted dropout

对于第l层神经元，设定保留神经元比例概率keep_prob=0.8，即该层有20%的神经元停止工作。
还要对输出al进行scale up处理。

Dropout为什么工作？

除此之外，还可以从权重w的角度来解释为什么dropout能够有效防止过拟合。对于某个神经元来说，某次训练时，它的某些输入在dropout的作用被过滤了。而在下一次训练时，又有不同的某些输入被过滤。经过多次训练后，某些输入被过滤，某些输入被保留。这样，该神经元就不会受某个输入非常大的影响，影响被均匀化了。也就是说，对应的权重w不会很大。这从从效果上来说，与L2 regularization是类似的，都是对权重w进行“惩罚”，减小了w的值。

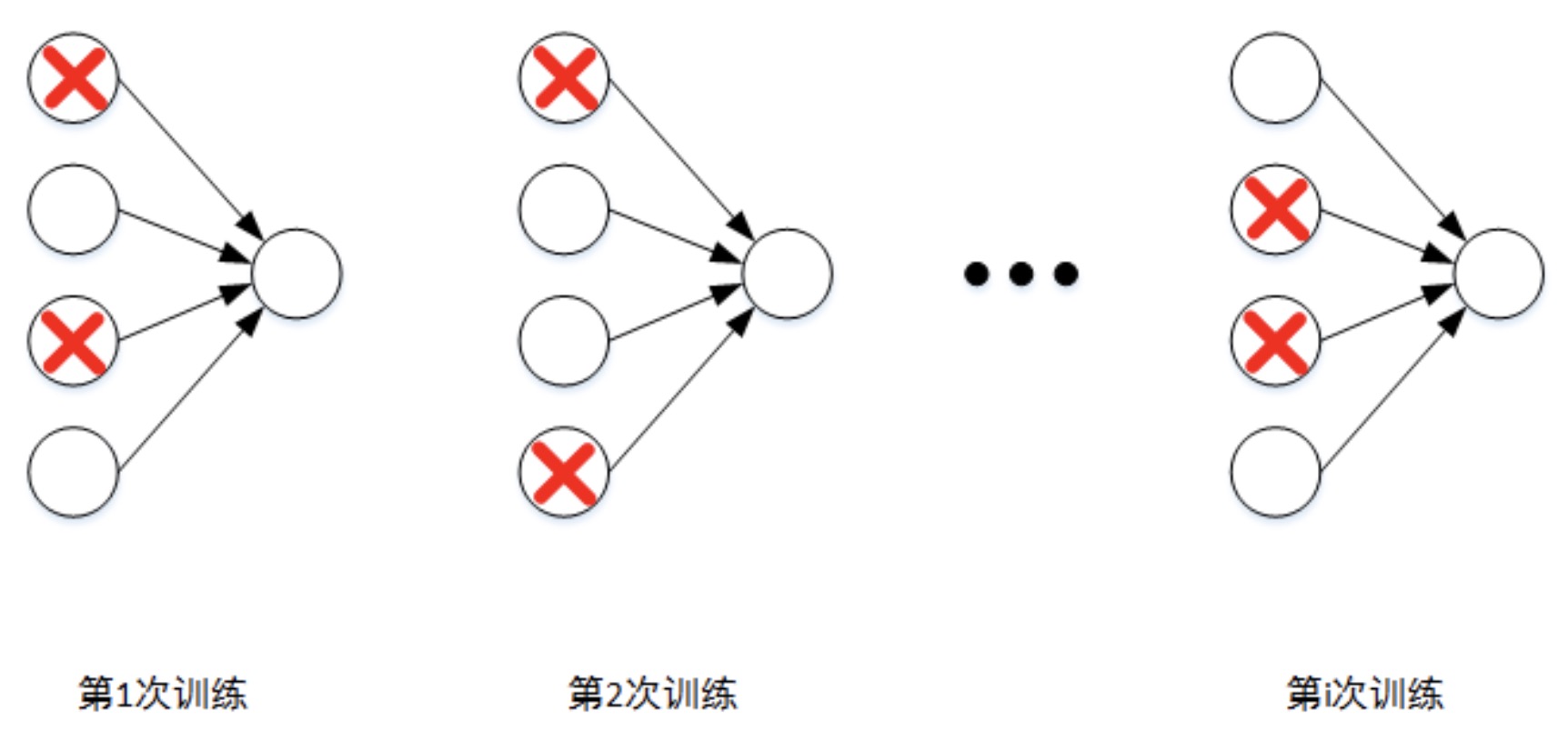
总结一下，对于同一组训练数据，利用不同的神经网络训练之后，求其输出的平均值可以减少overfitting。Dropout就是利用这个原理，每次丢掉一定数量的隐藏层神经元，相当于在不同的神经网络上进行训练，这样就减少了神经元之间的依赖性，即每个神经元不能依赖于某几个其他的神经元（指层与层之间相连接的神经元），使神经网络更加能学习到与其他神经元之间的更加健壮robust的特征。

注意点：

不同隐藏层的dropout系数keep_prob可以不同。一般来说，神经元越多的隐藏层，keep_out可以设置得小一些，例如0.5；神经元越少的隐藏层，keep_out可以设置的大一些，例如0.8。
建议对输入层进行dropout，如果输入层维度很大，例如图片，那么可以设置dropout，但keep_out应设置的大一些，例如0.8，0.9。
可以通过绘制cost function来进行debug，看看dropout是否正确执行。一般做法是，将所有层的keep_prob全设置为1，再绘制cost function，即涵盖所有神经元，看J是否单调下降。下一次迭代训练时，再将keep_prob设置为其它值。
最好只在需要regularization的时候使用dropout。

Normalizing inputs

\[\begin{array}{l}{\mu=\frac{1}{m} \sum_{i=1}^{m} X^{(i)}} \\ {\sigma^{2}=\frac{1}{m} \sum_{i=1}^{m}\left(X^{(i)}\right)^{2}} \\ {X :=\frac{X-\mu}{\sigma^{2}}}\end{array}\]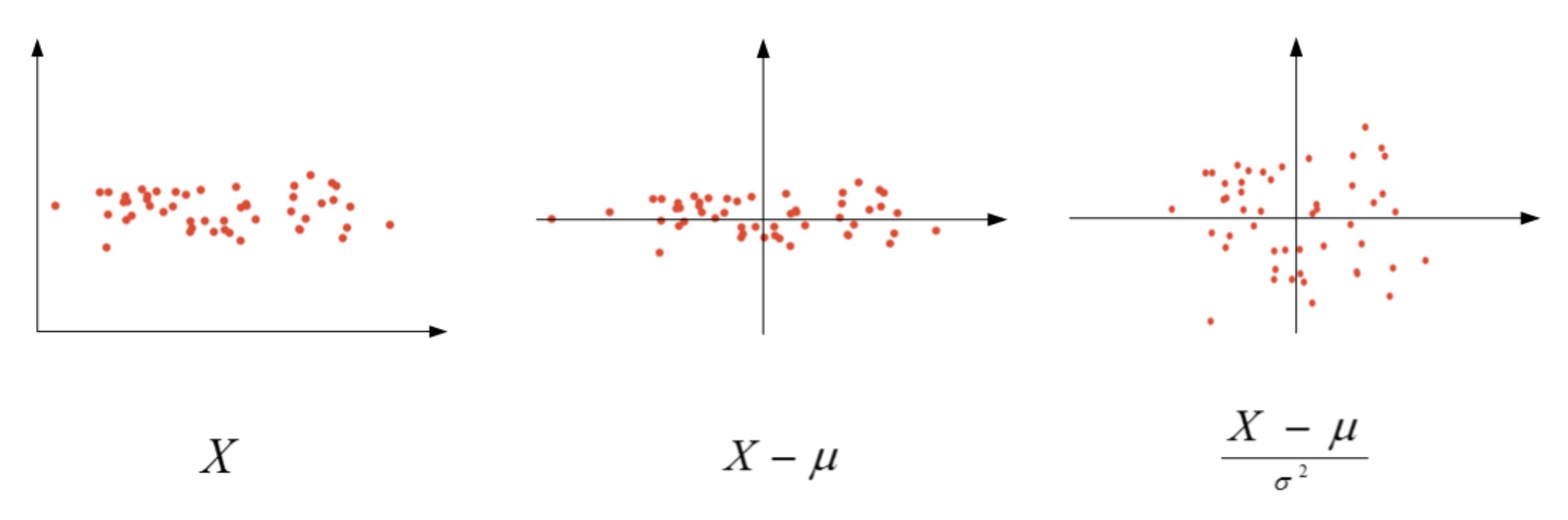

Vanishing and Exploding gradients

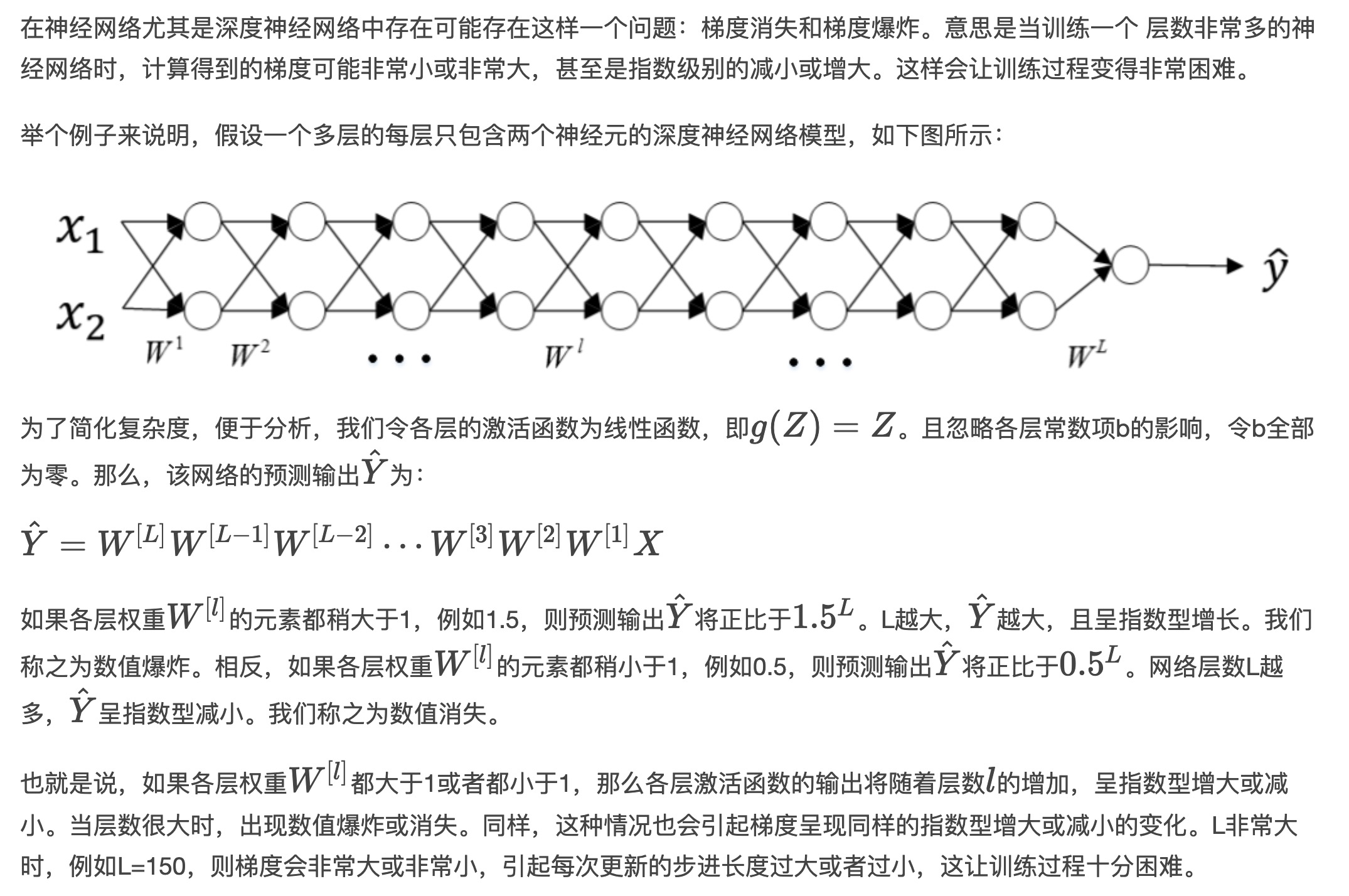
Weight Initialization for Deep Networks

1、权重初始化代码

2、Xavier与He初始化的推导

如果激活函数是tanh，一般选择如下的初始化方法。

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(1/n[l-1]) 

如果激活函数是ReLU，权重w的初始化一般令其方差为\(\frac2n\)：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(1/n[l-1]) 

除此之外，Yoshua Bengio提出了另外一种初始化w的方法，令其方差为\(\frac{2}{n^{[l-1]}n^{[l]}}\)：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1]*n[l]) 

He初始化基本思想是，当使用ReLU做为激活函数时，Xavier的效果不好，原因在于，当RelU的输入小于0时，其输出为0，相当于该神经元被关闭了，影响了输出的分布模式。

因此He初始化，在Xavier的基础上，假设每层网络有一半的神经元被关闭，于是其分布的方差也会变小。经过验证发现当对初始化值缩小一半时效果最好，故He初始化可以认为是Xavier初始/2的结果。

Gradient checking

见笔记：https://redstonewill.com/1052/

DeepLearning.ai-0201-正交化-正则化-Dropout-初始化

2019-07-19 深度学习课程