数据结构与算法 动态规划

动态规划（一）

2019-07-19 笔记

Posted by koko on July 19, 2019

[TOC]

动态规划（一）背包问题

注意：

1、边界问题

2、初始化

3、核心的地方在状态转移，比较偏数学

4、背包和贪心没有算法模版

复杂度的计算：

状态数量 * 转移的计算量

01 背包问题

题目描述

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 Ci，得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大。每件物品只能用一次，只能选择放与不放进背包。

状态表示与转移状态方程

image-20190718113630809

二维数组代码表示

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> v[i] >> w[i];
    }
    
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++) // 循环后面超过一行代码都记得打大括号
        {
            f[i][j] = f[i-1][j];
            if (j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
  
    return 0;  //don't forget
}

一维代码表示（滚动数组）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--) //思考下这里的构造，为什么要从大到小
        {
        f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
        
    cout << f[m] << endl;
    
    return 0;
}

完全背包问题

题目描述

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 Ci，得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大。每件物品有无限件。

状态转移方程

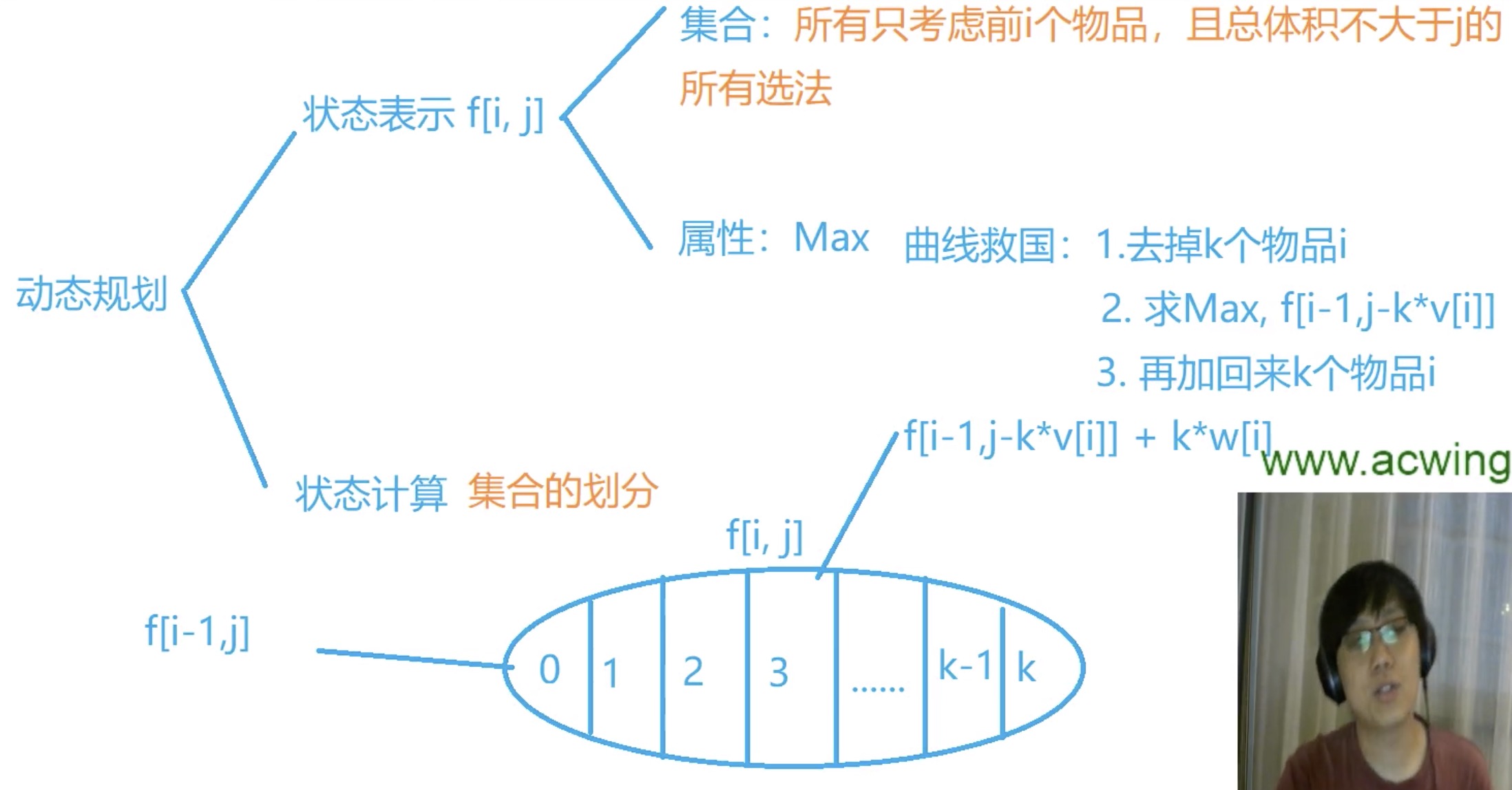
image-20190718151002353

朴素思想代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{

    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            for(int k = 0; k * v[i] <= j; k++ )
                f[i][j] = max( f[i][j] , f[i-1][j - k*v[i]] + k * w[i]);
    
    cout << f[n][m] << endl;
    return 0;

}

二维数组优化代码

image-20190718152403856

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{

    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0 ; j <= m; j++)
        {
            f[i][j] = f[i-1][j];
            if (j >= v[i]) f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;

}

再次优化到一维数组

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{

    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = v[i] ; j <= m; j++)
        {
           f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    cout << f[m] << endl;
    return 0;

}

多重背包问题

题目描述

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 Ci，得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大 。第i件物品最多有Si件可用。

状态转移方程

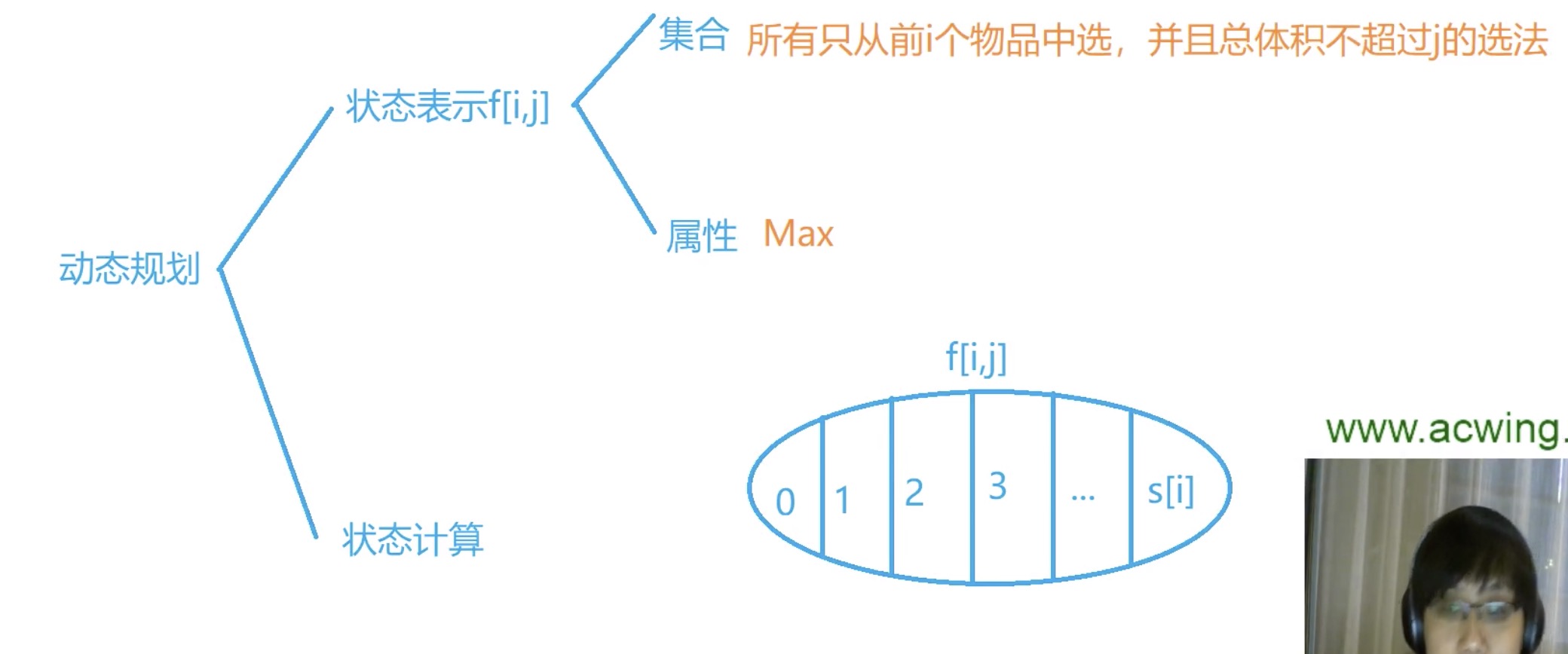
image-20190718172937254

暴力写法

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
    for(int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for(int k = 0; k <= s[i] && k * v[i] <= j; k++) //注意还要满足k*v[i] <= j
                f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*w[i]);
    
    cout << f[n][m] << endl;
    return 0;

}

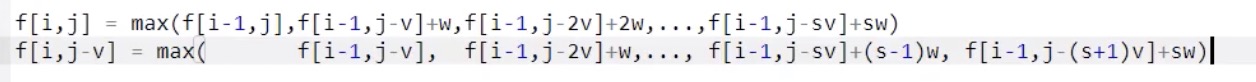
image-20190718172915268

优化方法（二进制）

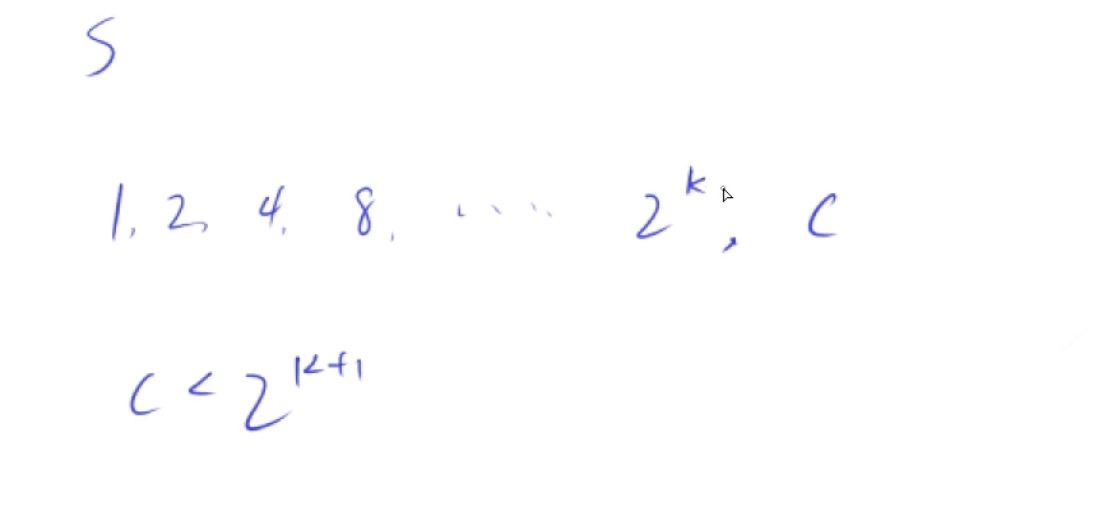
image-20190718173847335

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000;

int n, m;
int v[N], w[N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    //for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i]; 
    //如果先定义v[i]后面再操作的话，新的v[i]会覆盖后面的v[i]导致值不一样；
    int count = 0;
    
    for(int i = 1; i <= n; i++)
        {
            int a, b, s;
            cin >> a >> b >> s;
            int k = 1;
            while(k <= s)
            {   
                count++;
                v[count] = k * a;
                w[count] = k * b;
                s -= k;
                k = k * 2;
            }
            
            if( s > 0 )
            {
                count++;
                v[count] = s * a;
                w[count] = s * b;
            }
        }
    
    for(int i = 1; i <= count; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;

}

分组背包问题

题目描述

有 N 件物品和一个容量为 V 的背包。放入第 i 件物品耗费的费用是 Ci，得到的价值是 Wi。求解将哪些物品装入背包可使价值总和最大。这些物品被划为K组，每组中的物品互相冲突，只能选一件。

状态转移方程

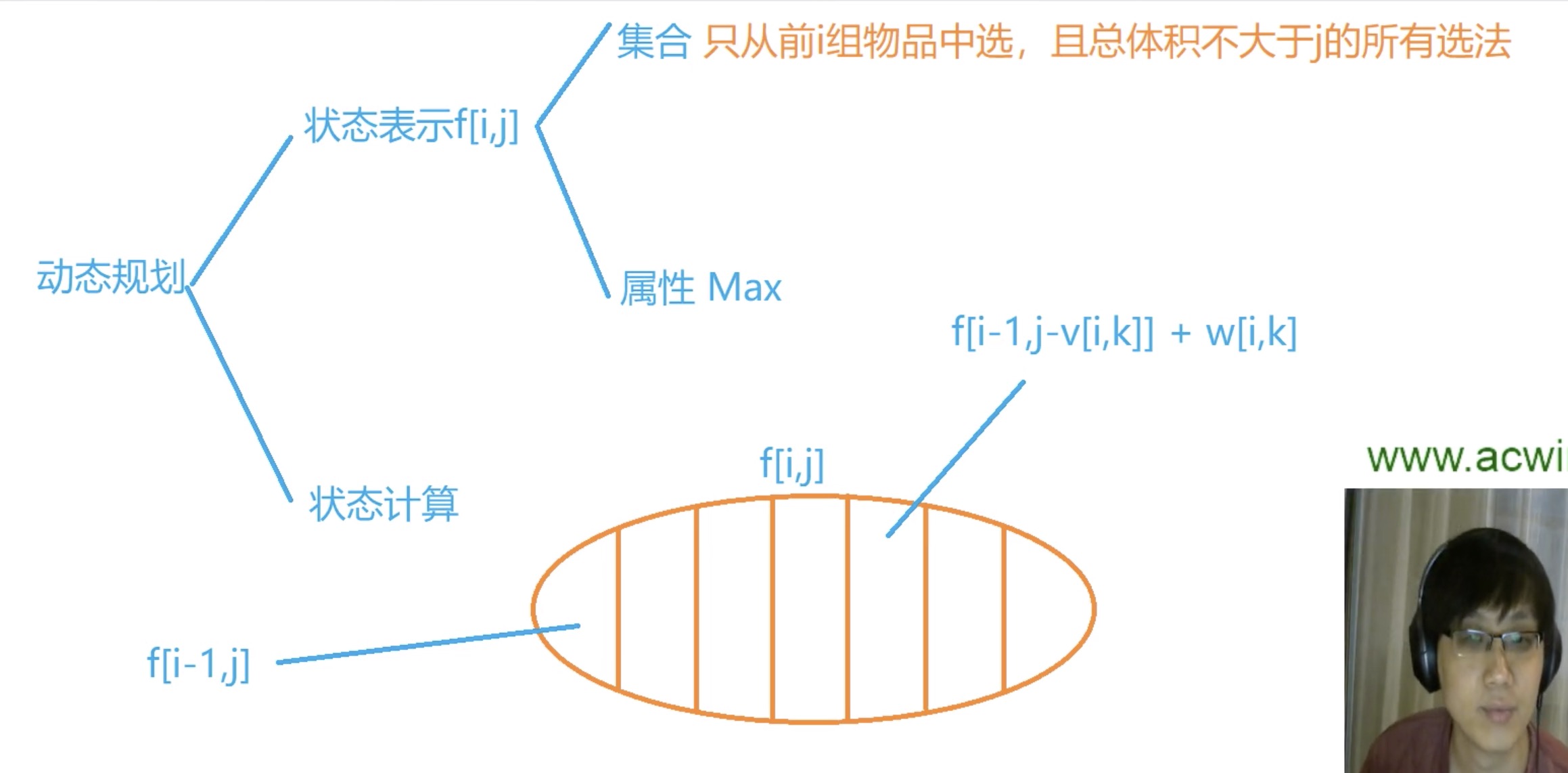
image-20190718183521954

二维数组代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int s[N];
int v[N][N], w[N][N];
int f[N][N];
    
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {   
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++ ) cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            for(int k = 1; k <= s[i]; k++)
            if(j >= v[i][k]) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
        }
    cout << f[n][m] << endl;
    
    return 0;
}

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int s[N];
int v[N][N], w[N][N];
//int f[N][N];
int f[N];
    
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {   
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++ ) cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= 0; j--)
            for(int k = 1; k <= s[i]; k++)
            {
                //f[i][j] = f[i - 1][j];
                //if( j >= v[i][k]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i][k]] + w[i][k]);
                if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
            }   
    cout << f[m] << endl;
    
    return 0;
}
CATALOG
    FEATURED TAGS
    Tool 深度学习 DeepLearning.ai 卷积神经网络 随记 书评 动态规划 数据结构与算法 Linux Paper
    FRIENDS