[TOC]
激活函数
Sigmoid
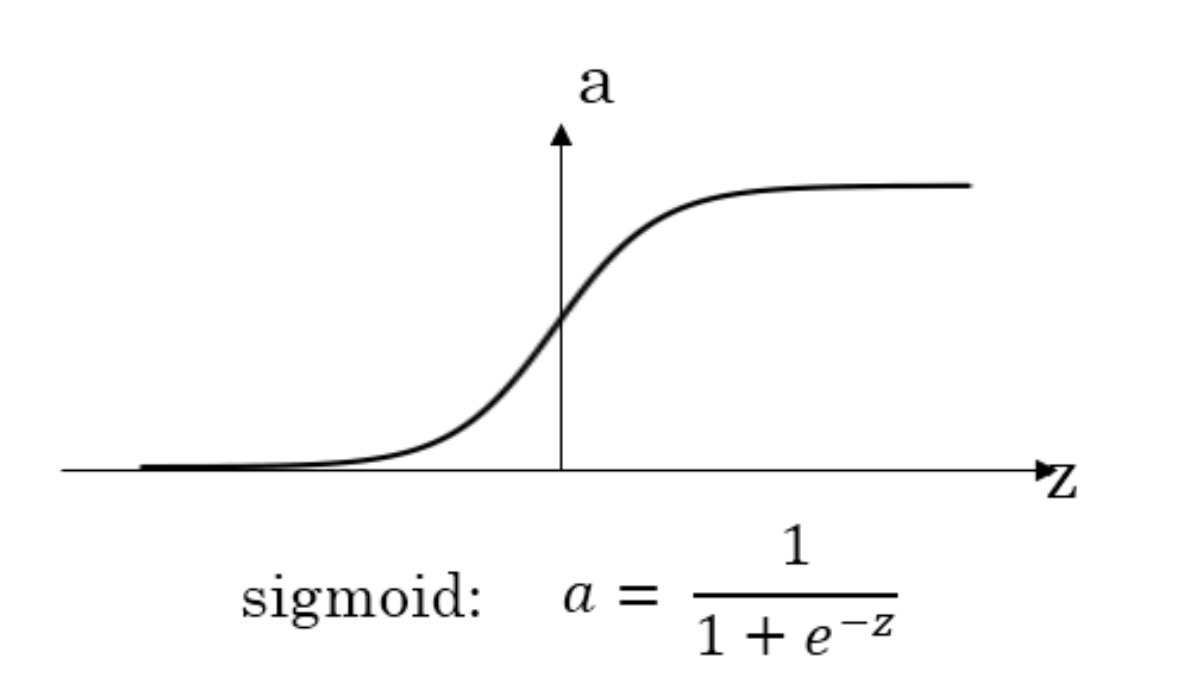
导数:
\(\begin{array}{l}{g(z)=\frac{1}{1+e^{(-2)}}} \\ {g^{\prime}(z)=\frac{d}{d z} g(z)=g(z)(1-g(z))=a(1-a)}\end{array}\) 求导过程:
tanh
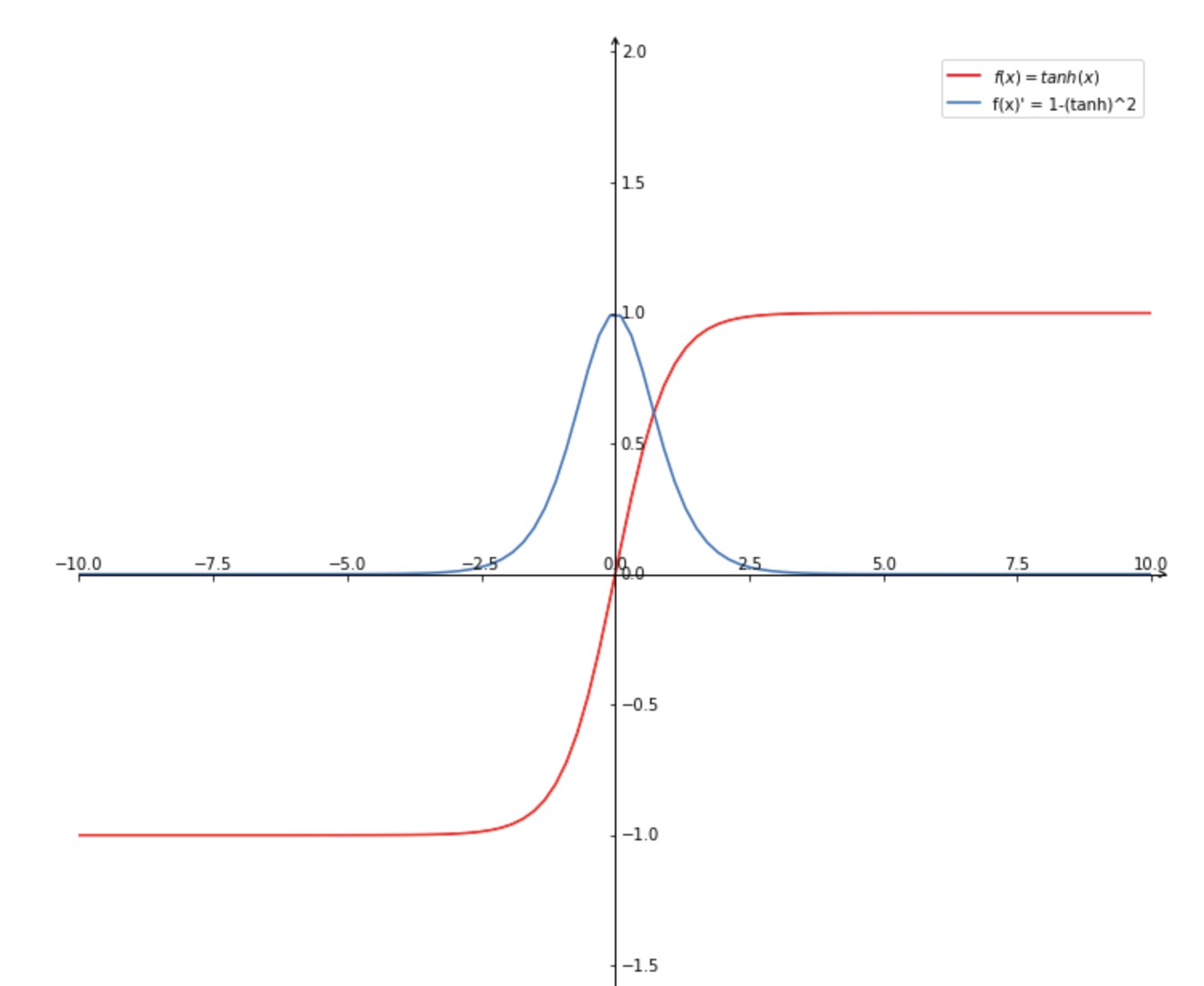
原函数与导数: \(\begin{array}{l}{g(z)=\frac{e^{(z)}-e^{(-z)}}{e^{(z)}+e^{-2} )}} \\ {g^{\prime}(z)=\frac{d}{d z} g(z)=1-(g(z))^{2}=1-a^{2}}\end{array}\)
作用:非常优秀,几乎适合所有的场景。
缺点:该导数在正负饱和区的梯度都会接近于 0 值,会造成梯度消失。还有其更复杂的幂运算。
Relu
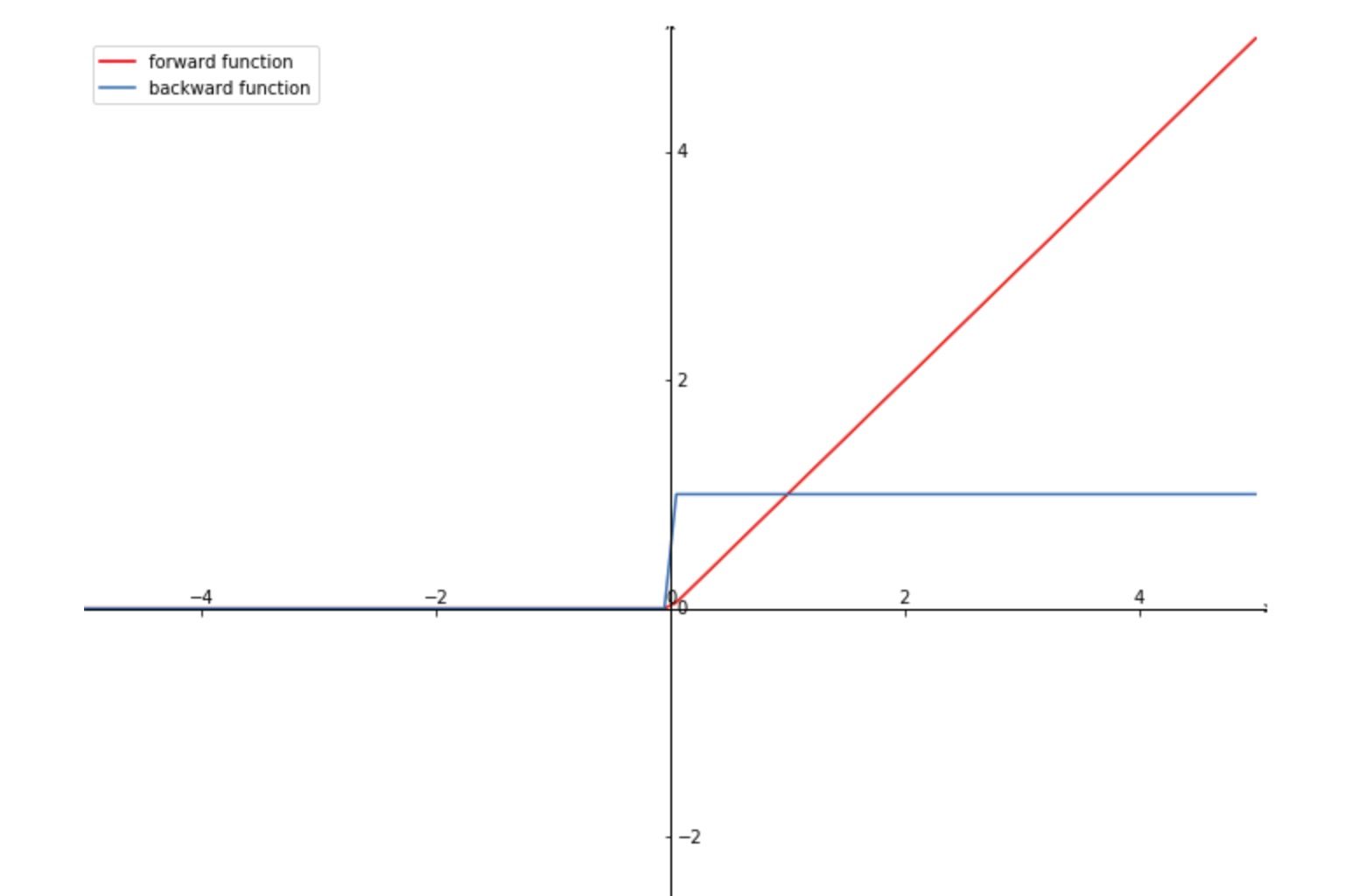
原函数:
\[f(x)=\left\{\begin{array}{ll}{0} & {\text { for } x<0} \\ {x} & {\text { for } x \geq 0}\end{array}\right.\]导数: \(f^{\prime}(x)=\left\{\begin{array}{ll}{0} & {\text { for } x<0} \\ {1} & {\text { for } x \geq 0}\end{array}\right.\)
一般作用:
- 大多数输出层
- 在不确定使用那个激活函数的情况下
- 隐含层也可以用到
优点:
- 比其他激活函数学习更快
- 不会产生梯度消失
缺点:
-
有些神经元会出现坏死现象,永远不会激活(可以使用 Leaky ReLu )
-
不会对数据进行压缩,会随着模型的层数增加而扩大
Leaky Relu
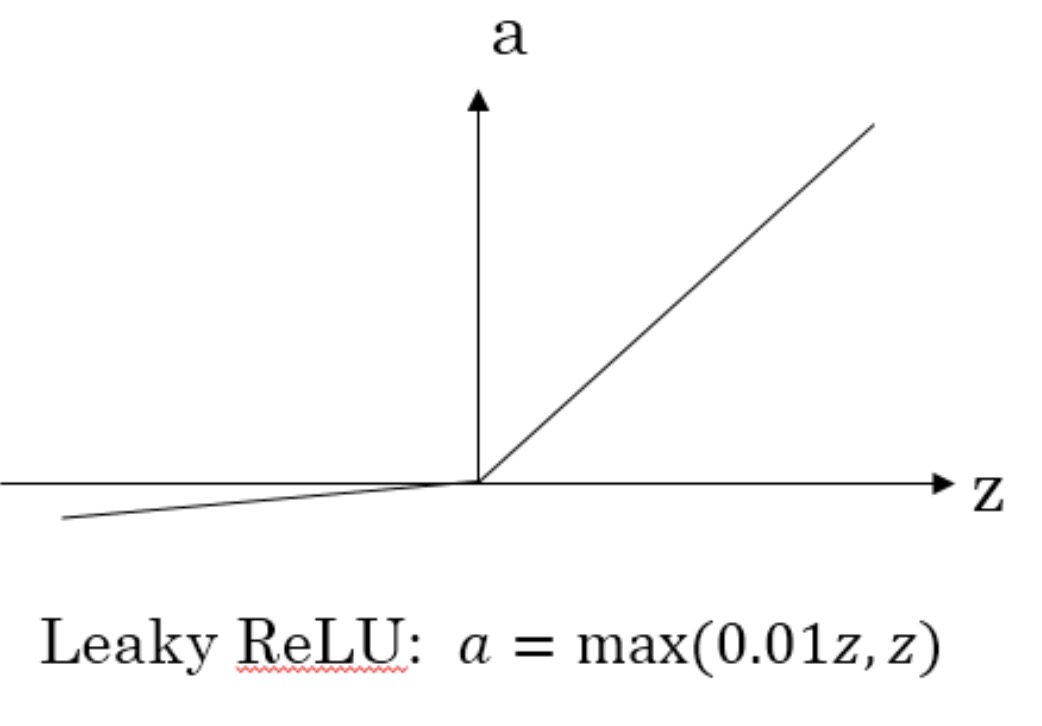
原函数:
\[f(x)=\left\{\begin{array}{ll}{0.01x} & {\text { for } x<0} \\ {x} & {\text { for } x \geq 0}\end{array}\right.\]导数: \(f^{\prime}(x)=\left\{\begin{array}{ll}{0.01} & {\text { for } x<0} \\ {1} & {\text { for } x \geq 0}\end{array}\right.\)
比较sigmoid、tanh、relu
sigmoid vs tanh
- 对于隐藏层的激活函数,tanh函数要比sigmoid函数表现更好一些:
因为tanh函数的取值范围在[-1,+1]之间,隐藏层的输出被限定在[-1,+1]之间,可以看成是在0值附近分布,均值为0。这样从隐藏层到输出层,数据起到了归一化(均值为0)的效果。
- 对于输出层的激活函数,因为二分类问题的输出取值为{0,+1},所以一般会选择sigmoid作为激活函数。
缺陷:
-
当 z 很大的时候,激活函数的斜率(梯度)很小。在这个区域内,梯度下降算法会运行得比较慢。在实际应用中,应尽量避免使z落在这个区域,使 z 尽可能限定在零值附近,从而提高梯度下降算法运算速度。
relu
为了弥补上述斜率变小的缺陷:
- ReLU激活函数在z大于零时梯度始终为1;
- 在z小于零时梯度始终为0;
- z等于零时的梯度可以当成1也可以当成0,实际应用中并不影响。
对于隐藏层,选择ReLU作为激活函数能够保证z大于零时梯度始终为1,从而提高神经网络梯度下降算法运算速度。
缺陷:
-
但当z小于零时,存在梯度为0的缺点,实际应用中,这个缺点影响不是很大。
-
为了弥补这个缺点,出现了Leaky ReLU激活函数,能够保证z小于零是梯度不为0。
能否使用线性激活函数?
推导过程
假设所有的激活函数都是线性的,为了简化计算,我们直接令激活函数\(g(z)=z\),即\(a=z\)。那么,浅层神经网络的各层输出为:
\[\begin{array}{l}{z^{[1]}=W^{[1]} x+b^{[1]}} \\ {a^{[1]}=z^{[1]}} \\ {z^{[2]}=W^{[2]} a^{[1]}+b^{[2]}} \\ {a^{[2]}=z^{[2]}}\end{array}\]我们对上式中\(a^{[2]}\)进行化简计算:
\[\begin{array}{l}{a^{[2]}=z^{[2]}=W^{[2]} a^{[1]}+b^{[2]}=W^{[2]}\left(W^{[1]} x+b^{[1]}\right)+b^{[2]}=\left(W^{[2]} W^{[1]}\right) x+\left(W^{[2]} b^{[1]}+\right.} \\ {b^{[2]} )=W^{\prime} x+b^{\prime}}\end{array}\]结论
经过推导我们发现\(a^{[2]}\)仍是输入变量x的线性组合。这表明,使用神经网络与直接使用线性模型的效果并没有什么两样。即便是包含多层隐藏层的神经网络,如果使用线性函数作为激活函数,最终的输出仍然是输入x的线性模型。这样的话神经网络就没有任何作用了。因此,隐藏层的激活函数必须要是非线性的。
另外,如果所有的隐藏层全部使用线性激活函数,只有输出层使用非线性激活函数,那么整个神经网络的结构就类似于一个简单的逻辑回归模型,而失去了神经网络模型本身的优势和价值。
值得一提的是,如果是预测问题而不是分类问题,输出y是连续的情况下,输出层的激活函数可以使用线性函数。如果输出y恒为正值,则也可以使用ReLU激活函数,具体情况,具体分析。